Hirschberg's Algorithmについて
問題
まず次の問題をご覧ください
概要:各マスに数字が書かれたグリッドが与えられ、そのグリッド上で左上のマスから右下のマスまで最短経路で移動することを考える。その通ったマスに書かれた数の総和を最小化せよ。また、その最小となる経路(の一例)を示せ。
愚直な解法
とりあえず総和の最小値を求めるだけなら左上から順番に次のような $DP$ をしていけばよいですね。
$dp(x, y) = grid(x, y) + min(dp(x - 1, y), dp(x, y - 1))$
グリッド上にこれを書き込むと以下のようになります。
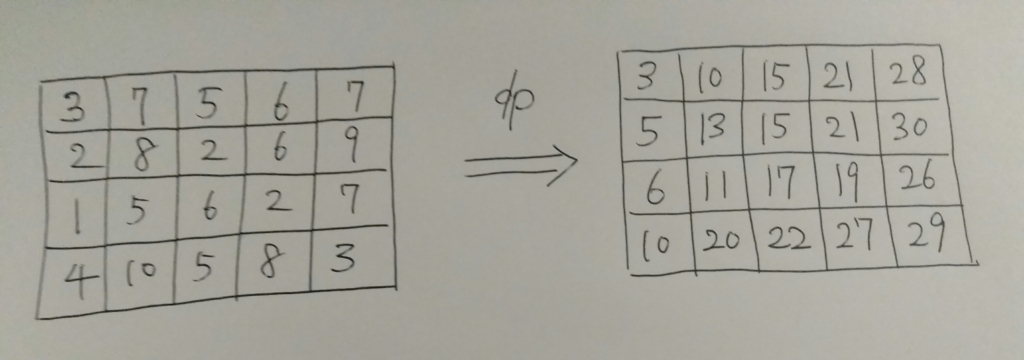
これで総和の最小値が $29$ であることがわかりました。次にこの経路の復元をしていきます。最短経路のあるマスにいるとき、その一歩手前に通ったマスというのは、左と上のマスのうち $DP$ の値($=$ そこまでの経路の総和)が小さい方なので、各マスについて左と上のどちらの $DP$ 値が大きいかを調べれば、後ろから復元することでができます。そこで、各マスについて左の方が小さい場合は $0$ 、上の方が小さい場合は $1$ を割り当てると画像の左のようになり、画像の右の経路が復元されます(ただしどちらかが存在しない場合は存在する方を小さいとみなします)。

とりあえず以上のことを実装すると以下のようになります。
vector<vector<long long>> dp(h, vector<long long> (w, INFL)); dp[0][0] = grid[0][0]; for (int i = 0; i < h; i ++) { for (int j = 0; j < w; j ++) { if (i - 1 >= 0) dp[i][j] = min(dp[i][j], (long long) grid[i][j] + dp[i - 1][j]); if (j - 1 >= 0) dp[i][j] = min(dp[i][j], (long long) grid[i][j] + dp[i][j - 1]); } } vector<bitset<10010>> restore(10010); for (int i = 0; i < h; i ++) { for (int j = 0; j < w; j ++) { if (i == 0) restore[i][j] = 0; else if (j == 0) restore[i][j] = 1; else restore[i][j] = dp[i - 1][j] < dp[i][j - 1]; } } int y = h - 1, x = w - 1; string ans = ""; while (true) { if (x == 0 && y == 0) break; if (restore[y][x]) { ans += "D"; y --; } else { ans += "R"; x --; } } reverse(ans.begin(), ans.end()); cout << ans << endl;
ここまでで前置きはおしまいです。
問題点
さて、もとの問題をもう一度よく読んで見ると、$ML$ が $5120 KB$ となっています。これは割と厳しい制約で、各数値が書かれたグリッドの配列を用意する(空間計算量 $= O(HW)$ )ことが許されていません(各マスの値が変な計算式で与えられていたのはこのためです)。
総和の最小値だけなら、$DP$ 配列を使い回すことで、同じ計算量で $2$ 列分ずつ計算していくことができます。しかし、経路の復元はどのようにすればよいでしょうか。
考えられる方法の一つ目としてはまず左端から $2$ 列分ずつ復元を考慮しながら遷移していく方法ですが、右の $DP$ の結果によってどの経路を採用するかは全く決めることができないことから、結局 $O(HW)$ となってしまうのでダメそうです。
次に右端から $2$ 列分ずつ復元をしていく方法ですが、これならメモリは $O(min(H, W))$ で済みそうです。しかし、$ DP $値の保存はできないことから、右から順に $2$ 列分を見るたびに左端から計算をしなければいけないので、時間計算量が $O(HW * min(H, W))$ になってしまって、今度は時間が間に合わなさそうです。
解決策
そこで $Hirschberg's\ Algorithm$ の登場です。これはこの経路復元を時間計算量 $O(HW)$ を維持したまま、空間計算量を $O(min(H, W))$ に落とすアルゴリズムです。
このアルゴリズムは分割統治法の考え方に基づいています。すなわち、グリッドを分割して、それぞれで経路を求めてマージします。
まずグリッドを $2$ 分割します。そしてその $2$ つのグリッドの間で、左から右に移動する位置がちょうど一つ存在するので、それを求めます。
それを求めるには、左のグリッドでは左上から右下に向かう $DP$ 、右のグリッドでは右下から左上に向かう $DP$ をします。さっきの例では次のように計算できます。
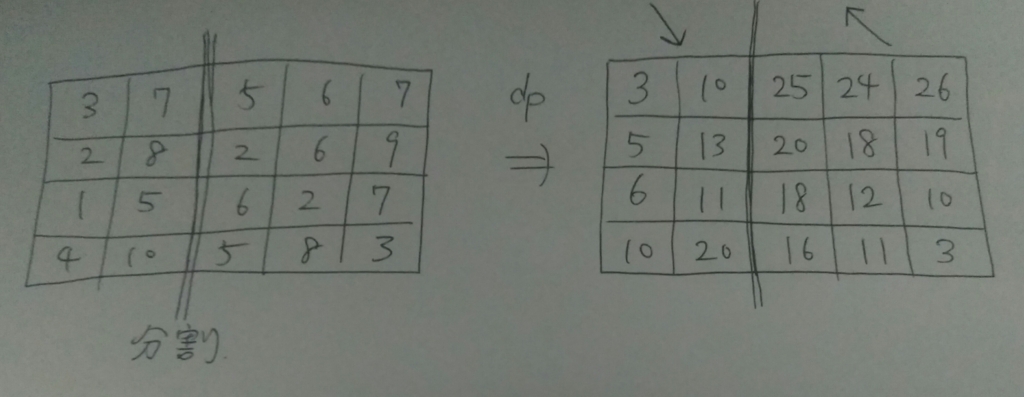
この結果、分割した位置の各高さについて、左上からの最短距離と右下からの最短距離が計算されたので、これらの和が最も小さい部分が最短経路になるはずです。上の図では、この和は上から順に $35, 33, 29, 36$ となっているので、上から $3$ 段目が最短経路の一部であることがわかります。
さて、この分割を繰り返していくのですが、右端から見ていく計算と何が違うのかは、$2$ 回目に見る必要があるグリッドのサイズを見ればわかると思います。$2$ 回目に見るグリッドは、移動の方向が右か下しかないことから、次の部分だけでよいはずです。
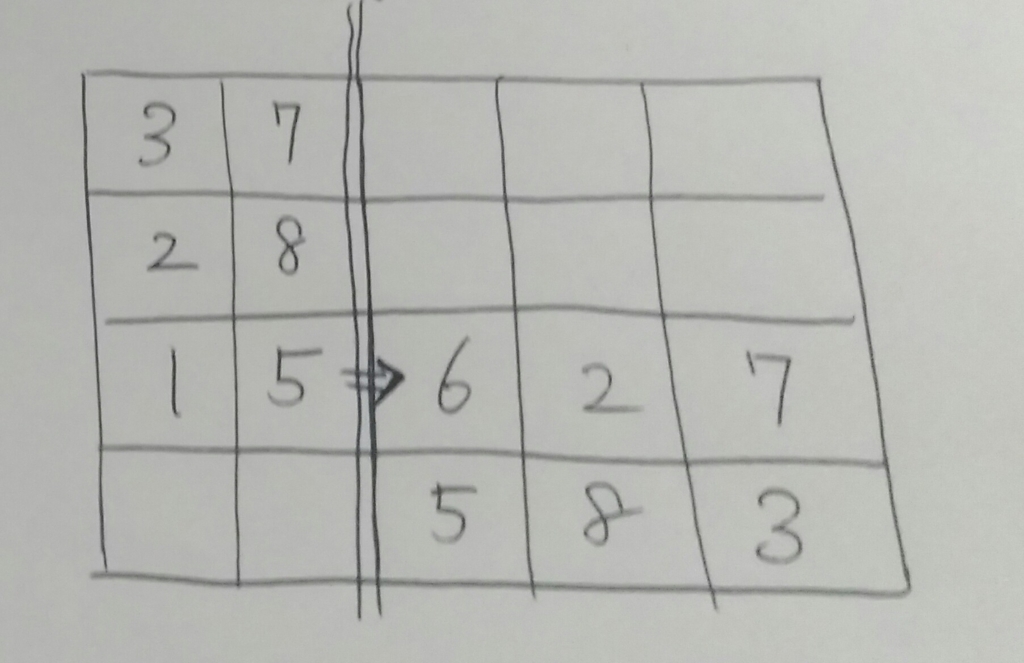
これはなにを言っているのかというと、$k$ 回目の計算量は $k - 1$ 回目の計算量のおよそ半分になっているということです。同様にして例えば $3$ 回目の計算は以下のような全体の $\cfrac{1}{4}$ の領域だけ見ればよいことがわかります。
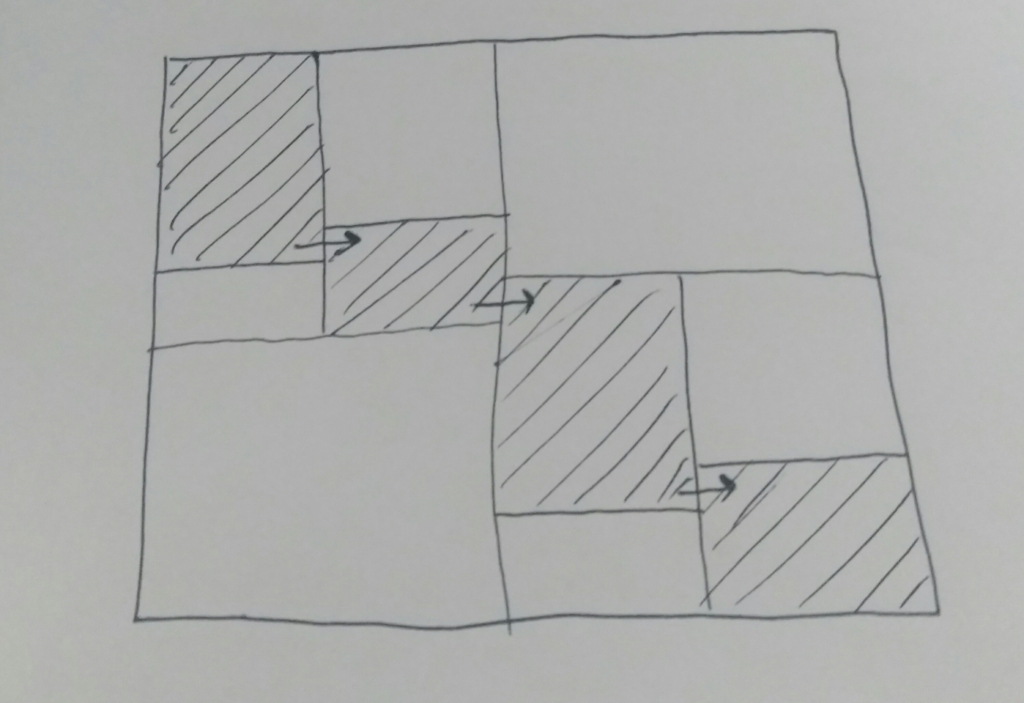
さて、この全体の計算量についてですが、まず空間については上にも述べたように配列を使いまわすことで、$O(min(H, W))$ で抑えられます。一方時間計算量は、一番最初の計算が $O(HW)$ で、その後半分ずつになっていくので、全体としては $O(HW(1 + \cfrac{1}{2} + \cfrac{1}{4} + ...)) = O(HW * 2) = O(HW)$ となります。これで時間計算量を維持したまま、空間計算量を落とすことができました。
以上でアルゴリズムの説明は終わりです。実装上の注意としては、各位置を全体の位置との相対位置できちんと把握する点くらいだと思います。以下の実装では、スワップが面倒なので空間計算量 $O(min(H, W))$ ではなく、$O(W)$ で計算しています。
実装例
#include <iostream> #include <cstdio> #include <algorithm> #include <vector> #include <functional> #include <string> using namespace std; template<class T> void amin(T &a, T b) { if (a > b) a = b; } int main() { int h, w; scanf("%d%d", &h, &w); vector<int> u(h), v(w); for (int i = 0; i < h; i ++) scanf("%d", &u[i]); for (int i = 0; i < w; i ++) scanf("%d", &v[i]); function<long long (int, int)> get_val = [&](int i, int j) { return (long long) (u[i] + j + 1) ^ (long long) (v[j] + i + 1); }; //Hirschberg vector<pair<int, int>> pos; function<void (int, int, int, int)> Hirschberg = [&](int li, int lj, int ri, int rj) { int mid = (lj + rj) / 2; int height = ri - li + 1; if (rj - lj < 1) return; if (height == 1) { pos.emplace_back(mid, li); Hirschberg(li, lj, li, mid); Hirschberg(li, mid + 1, li, rj); return; } //left int w_left = mid - lj + 1; vector<vector<long long>> dp(2, vector<long long> (height)); dp[0][0] = get_val(li, lj); for (int i = 1; i < height; i ++) { dp[0][i] = dp[0][i - 1] + get_val(li + i, lj); } bool f = 1; for (int j = 1; j < w_left; j ++) { for (int i = 0; i < height; i ++) { dp[f][i] = 1LL << 60; } for (int i = 0; i < height; i ++) { int val = get_val(li + i, lj + j); amin(dp[f][i], dp[!f][i] + val); if (i - 1 >= 0) amin(dp[f][i], dp[f][i - 1] + val); } f = !f; } f = !f; vector<long long> m1(height); for (int i = 0; i < height; i ++) { m1[i] = dp[f][i]; } //right int w_right = rj - mid; dp[0][0] = get_val(ri, rj); for (int i = 1; i < height; i ++) { dp[0][i] = dp[0][i - 1] + get_val(ri - i, rj); } f = 1; for (int j = 1; j < w_right; j ++) { for (int i = 0; i < height; i ++) { dp[f][i] = 1LL << 60; } for (int i = 0; i < height; i ++) { long long val = get_val(ri - i, rj - j); amin(dp[f][i], dp[!f][i] + val); if (i - 1 >= 0) amin(dp[f][i], dp[f][i - 1] + val); } f = !f; } f = !f; vector<long long> m2(height); for (int i = 0; i < height; i ++) { m2[height - i - 1] = dp[f][i]; } // long long mi = 1LL << 60; int res = -1; for (int i = 0; i < height; i ++) { long long sum = m1[i] + m2[i]; if (sum < mi) { mi = sum; res = i; } } res += li; pos.emplace_back(mid, res); Hirschberg(li, lj, res, mid); Hirschberg(res, mid + 1, ri, rj); }; Hirschberg(0, 0, h - 1, w - 1); // sort(pos.begin(), pos.end()); int y = 0, x = 0; string ans = ""; while (true) { if (x == w - 1) { while (y != h - 1) { ans += "D"; y ++; } break; } if (pos[x].second == y) { x ++; ans += "R"; } else { y ++; ans += "D"; } } cout << ans << endl; return 0; }